The Burr family of distributions has been used extensively for over 20 years as a species sensitivity distribution (SSD) in ecotoxicology. Indeed, its popularity (at least in Australia and New Zealand) has been guaranteed by the fact that it is a default distribution in the Burrlioz software tool which underpins the methodology for guideline development (GV) in those countries.
The main advantages of the Burr distributions are (i) they can accommodate a wide variety of distributional shapes; and (ii) the cdf is readily inverted to provide a closed-form solution for percentile estimates (aka HCx values).
The down-side however, is that many toxicity data sets have characteristics that can result in numerical instabilities when maximum likelihood approaches are used to estimate the parameters of a Burr distribution. The problem is most acute when attempting to fit a 3-parameter Burr distribution to small toxicity data sets that are highly skewed (statisticians would walk away from such situations, but unfortunately, this is the norm in ecotoxicology).
We have recently been undertaking research into alternative estimation strategies and/or re-parameterising the Burr distributions to overcome these computational issues. A promising alternative to the use of maximum likelihood is estimation using L-Moments.
We have developed a simple, graphical-based method for the L-Moment estimation of the parameters of a Burr III distribution. The video below explains.
So what does this distribution look like and how does it compare to that obtained using MLEs? Figure 1 below says it all – the fits are very similar over the entire range of concentrations and almost identical where it matters – in the left tail and this is reflected in the HCx estimates of Table 1.
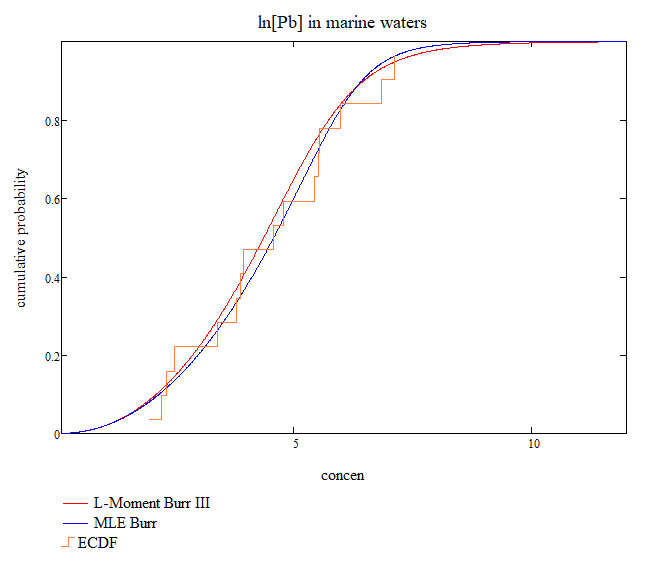
| Burr III parameters: {b,c,k} | HC1 | HC5 | HC10 |
|---|---|---|---|
| MLE {6.304,11.932,0.180} | 0.737 | 1.560 | 2.155 |
| L-Moments {5.896,8.148,0.273} | 0.744 | 1.534 | 2.095 |